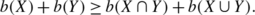GraphCliques
- SI: GraphCliques
- Open access
- Published:
Sandwich problems on orientations
Journal of the Brazilian Computer Society volume 18, pages 85–93 (2012)
Abstract
The graph sandwich problem for property Π is defined as follows: Given two graphs G1=(V,E1) and G2=(V,E2) such that E1⊆E2, is there a graph G=(V,E) such that E1⊆E⊆E2 which satisfies property Π? We propose to study sandwich problems for properties Π concerning orientations, such as Eulerian orientation of a mixed graph and orientation with given in-degrees of a graph. We present a characterization and a polynomial-time algorithm for solving the m-orientation sandwich problem.
1 Introduction
Given two graphs G1=(V,E1) and G2=(V,E2) with the same vertex set V and E1⊆E2, a graph G=(V,E) is called a sandwich graph for the pair G1,G2 if E1⊆E⊆E2. The graph sandwich problem for property Π is defined as follows [12]:
Graph Sandwich Problem for Property Π Instance: Given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2. Question: Is there a graph G=(V,E) such that E1⊆E⊆E2 and G satisfies property Π?
We call E1 the mandatory edge set, E0=E2∖E1 the optional edge set and E3 the forbidden edge set, where E3 denotes the set of edges of the complementary graph \(\overline{G}_{2}\) of G2. Thus any sandwich graph G=(V,E) for the pair G1,G2 must contain all mandatory edges, no forbidden edges and may contain a subset of the optional edges. Graph sandwich problems have attracted much attention lately arising from many applications and as a natural generalization of recognition problems [1–3, 7, 22, 24]. The recognition problem for a class of graphs \(\mathcal{C}\) is equivalent to the graph sandwich problem in which G1=G2=G, where G is the graph we want to recognize and property Π is “to belong to class \(\mathcal{C}\)”.
In this paper we propose to study sandwich problems for properties Π concerning orientations, such as Eulerian orientation of a mixed graph and orientation with given in-degrees of a graph, or more generally of a mixed graph.
The paper is organized as follows: Sect. 2 contains some basic definitions, notations and results. Section 3 contains some known results on degree constrained sandwich problems. We consider the undirected version and the directed version, the complexity, the characterization and the related optimization problems. We also define a simultaneous version and discuss its complexity. Section 4 focuses on Eulerian sandwich problems. We consider first undirected graphs and then directed graphs. These problems were already solved in [12], here we point out that the undirected case reduces to T-joins, while the directed case to circulations. We discuss the complexity of the problems and their characterizations and we also propose some mixed versions. In Sect. 5 we consider sandwich problems regarding an m-orientation, i.e., given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2 and a non-negative integer vector m on V, we show that it is polynomial to decide whether there exists a sandwich graph G=(V,E) (E1⊆E⊆E2) that has an orientation \(\vec{G}\) whose in-degree vector is m that is \(d^{-}_{\vec{G}}(v)=m(v)\) for all v∈V. This result stands in contrast to the strongly connected m-orientation sandwich problem which we show is NP-complete. Section 6 is devoted to a new kind of sandwich problem where we may contract (and not delete) optional edges and property Π is being bipartite.
2 Definitions
- Undirected graphs :
-
Let G=(V,E) be an undirected graph. For vertex sets X and Y, the cut induced by X is defined to be the set of edges of G having exactly one end-vertex in X and is denoted by
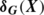 . The degree
. The degree (or d
E
(X)) of X is the cardinality of the cut induced by X, that is, d
G
(X)=|δ
G
(X)|. The number of edges between X∖Y and Y∖X is denoted by
(or d
E
(X)) of X is the cardinality of the cut induced by X, that is, d
G
(X)=|δ
G
(X)|. The number of edges between X∖Y and Y∖X is denoted by  . The number of edges of G having both (resp. at least one) end-vertices in X is denoted by
. The number of edges of G having both (resp. at least one) end-vertices in X is denoted by  or i
E
(X) or simply i(X) (resp.
or i
E
(X) or simply i(X) (resp.  ). It is well-known that (1) is satisfied for all X,Y⊆V,
). It is well-known that (1) is satisfied for all X,Y⊆V,  (1)
(1)
We say that a vector m on V is the degree vector of G if d
G
(v)=m(v) for all v∈V. For a vector m on V, we consider m as a modular function, that is, we use the notation  . Let us recall that d
G
(X) is the degree function of G. We define
. Let us recall that d
G
(X) is the degree function of G. We define  as the modular function defined by the degree vector d
G
(v) of G. Note that \(\hat{d}_{G}(X)=d_{G}(X)+2i_{G}(X)\forall X\subseteq V\).
as the modular function defined by the degree vector d
G
(v) of G. Note that \(\hat{d}_{G}(X)=d_{G}(X)+2i_{G}(X)\forall X\subseteq V\).
We denote by  the set of vertices of G of odd degree. For an edge set F of G, the subgraph induced by F, that is, (V,F), is denoted by
the set of vertices of G of odd degree. For an edge set F of G, the subgraph induced by F, that is, (V,F), is denoted by  . We say that G is Eulerian if the degree of each vertex is even, that is, if T
G
=∅. Note that we do not suppose the graph to be connected.
. We say that G is Eulerian if the degree of each vertex is even, that is, if T
G
=∅. Note that we do not suppose the graph to be connected.
Let T be a vertex set in G. An edge set F of G is called T-join if the set of odd degree vertices in the subgraph induced by F coincide with T, that is if TG(F)=T. Given a cost vector on the edge set of G, a minimum cost T-join can be found in polynomial time by Edmonds and Johnson’s algorithm [5].
Let f be a non-negative integer vector on V. An edge set F of G is called an f-factor of G if f is the degree vector of G(F), that is, d F (v)=f(v) for all v∈V. If f(v)=1 for all v∈V, then we say that F is a 1-factor or a perfect matching. An f-factor—if it exists—can be found in polynomial time, see [20]. The graph G is called 3-regular if each vertex is of degree 3. Note that for a 3-regular graph, the existence of two edge-disjoint perfect matchings is equivalent to the existence of three edge-disjoint perfect matchings which is equivalent to the 3-edge-colorability of the graph.
- Directed graphs :
-
Let D=(V,A) be a directed graph. For a vertex set X, the set of arcs of D entering (resp. leaving) X is denoted by
 (resp.
(resp. 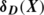 ). The in-degree
). The in-degree (resp. out-degree
(resp. out-degree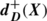 ) of X is the number of arcs of D entering (resp. leaving) X, that is \(d^{-}_{D}(X)=|\varrho _{D}(X)|\) (resp. \(d^{+}_{D}(X)=|\delta_{D}(X)|\)). The set of arcs of G having both end-vertices in X is denoted by
) of X is the number of arcs of D entering (resp. leaving) X, that is \(d^{-}_{D}(X)=|\varrho _{D}(X)|\) (resp. \(d^{+}_{D}(X)=|\delta_{D}(X)|\)). The set of arcs of G having both end-vertices in X is denoted by  . The following equality will be used frequently without reference:
. The following equality will be used frequently without reference:  (2)
(2)
We say that a vector m on V is the in-degree vector of D if \(d^{-}_{D}(v)=m(v)\) for all v∈V. Let us recall that \(d^{-}_{D}(X)\) is the in-degree function of D. Let f be a non-negative integer vector on V. An arc set F of D is called a directedf-factor of D if f is the in-degree vector of D(F), that is, \(d^{-}_{F}(v)=f(v)\) for all v∈V.
We say that D is Eulerian if the in-degree of v is equal to the out-degree of v for all v∈V, that is, \(d^{-}_{D}(v)=d^{+}_{D}(v)\) for all v∈V. Note that we do not suppose the graph to be connected.
Let f and g be two vectors on the arcs of D such that f(e)≤g(e) for all e∈A. A vector x on the arcs of D is a circulation if (3) and (4) are satisfied.


Note that if f(e)=g(e)=1 for all e∈A, then D is Eulerian if and only if f is a circulation. We will use the following characterization when a circulation exists.
Theorem 1
(Hoffmann [15])
LetD=(V,A) be a directed graph andfandgtwo vectors onAsuch thatf(e)≤g(e)∀e∈A. There exists a circulation inDif and only if

We say that H=(V,E∪A) is a mixed graph if E is an edge set and A is an arc set on V. For an undirected graph G=(V,E), if we replace each edge uv by the arc uv or vu, then we get the directed graph  . We say that \(\vec{G}\) is an orientation of G.
. We say that \(\vec{G}\) is an orientation of G.
Mixed graphs having Eulerian orientations are characterized as follows.
Theorem 2
(Ford, Fulkerson [8])
A mixed graphH=(V,E∪A) has an Eulerian orientation if and only if


The following theorem characterizes graphs having an orientation with a given in-degree vector.
Theorem 3
(Hakimi [13])
Given an undirected graphG=(V,E) and a non-negative integer vectormonV, there exists an orientation\(\vec{G}\)ofGwhose in-degree vector ismif and only if


- Functions :
-
Let b be a set function on the subsets of V. We say that b is submodular if for all X,Y⊆V,
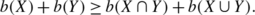 (10)
(10)
The function b is called supermodular if −b is submodular. A function is modular if it is supermodular and submodular. We will use frequently in this paper the following facts.
Claim 1
The degree functiond G (Z) of an undirected graphGand the in-degree function\(d^{-}_{D}(Z)\)of a directed graphDare submodular and the functioni(Z) is supermodular.
Theorem 4
The minimum value of a submodular function can be found in polynomial time.
Theorem 5
(Frank [9])
Letbandpbe a submodular and a supermodular set function onVsuch thatp(X)≤b(X) for allX⊆V. Then there exists a modular functionmonVsuch thatp(X)≤m(X)≤b(X) for allX⊆V. Ifbandpare integer valued thenmcan also be chosen integer valued.
A pair (p,b) of set functions on 2V is a strong pair if p (resp. b) is supermodular (submodular) and they are compliant, that is, for every pairwise disjoint triple X,Y,Z,
Note that a pair (α,β) of modular functions is a strong pair if and only if α≤β. If (p,b) is a strong pair then the polyhedron

is called a generalized polymatroid (or a g-polymatroid). When α≤β are modular, we also call the g-polymatroid Q(α,β) a box.
Theorem 6
(Frank, Tardos [11])
The intersection of an integral g-polymatroidQ(p,b) and an integral boxQ(α,β) is an integral g-polymatroid. It is nonempty if and only ifα≤bandp≤β.
- Matroids :
-
A set system \(M=(V,{\mathcal{F}})\) is called a matroid if \({\mathcal{F}}\) satisfies the following three conditions:
-
(I1)
\(\emptyset\in{\mathcal{F}}\),
-
(I2)
if \(F\in{\mathcal{F}}\) and F′⊆F, then \(F'\in{\mathcal{F}}\),
-
(I3)
if \(F, F'\in{\mathcal{F}}\) and |F|>|F′|, then there exists f∈F∖F′ such that \(F'\cup f\in{\mathcal{F}}\).
-
(I1)
A subset X of V is called independent in M if \(X\in{\mathcal{F}}\), otherwise it is called dependent. The maximal independent sets of V are the basis of M. Let \({\mathcal{B}}\) be the set of basis of M. Then \({\mathcal{B}}\) satisfies the following two conditions:
-
(B1)
\({\mathcal{B}}\neq\emptyset\),
-
(B2)
if \(B, B'\in{\mathcal{B}}\) and b∈B∖B′, then there exists b′∈B′∖B such that \((B-b)\cup b'\in{\mathcal{B}}\).
Conversely, if a set system \((V,{\mathcal{B}})\) satisfies (B1) and (B2), then \(M=(V,{\mathcal{F}})\) is a matroid, where \({\mathcal{F}}=\{F\subseteq V:\exists B\in{\mathcal{B}}, F\subseteq B\}\).
For S⊂V, the matroid M∖S obtained from M by deletingS is defined as \(M\setminus S=(V\setminus S, {\mathcal{F}}|_{V\setminus S})\), where X⊆V∖S belongs to \({\mathcal{F}}|_{V\setminus S}\) if and only if \(X\in{\mathcal{F}}\). For \(S\in{\mathcal{F}}\), the matroid M/S obtained from M by contractingS is defined as \(M/S=(V\setminus S, {\mathcal{F}}_{S})\), where X⊆V∖S belongs to \({\mathcal{F}}_{S}\) if and only if \(X\cup S\in{\mathcal{F}}\). Let {V1,…,V l } be a partition of V and a1,…,a l a set of non-negative integers. Then \(M=(V,{\mathcal{F}})\) is a matroid, where \({\mathcal{F}}=\{F\subseteq V: |F\cap V_{i}|\leq a_{i}\}\), we call it partition matroid. The dual matroid M∗ of M is defined as follows: the basis of M∗ are the complements of the basis of M.
Let \(M=(V,{\mathcal{F}})\) be a matroid and c a cost vector on V={v1,…,v n }. We can find a minimum cost basis F n of M in polynomial time by the greedy algorithm: take a non-decreasing order of the elements of V:c(v1)≤…≤c(v n ). Let F0 be empty and for i=1,…,n, let F i =Fi−1+v i if \(F_{i-1}+v_{i}\in {\mathcal{F}}\), otherwise let F i =Fi−1.
If M1 and M2 are two matroids on the same ground set V, then we can find a common basis of M1 and M2 in polynomial time (if there exists one) by the matroid intersection algorithm of Edmonds [4].
Theorem 7
(Edmonds, Rota [18])
For an integer-valued, non-decreasing, submodular functionbdefined on a ground setS, the set {F⊆S;|F′|≤b(F′) for all ∅≠F′⊆F} forms the set of independent sets of a matroidM b whose rank functionr b is given by
Given an undirected graph G=(V,E) and a non-negative integer vector m on V, let \(\bar{m}^{G}=\bar{m}\) be the set function defined on E by \(\bar{m}(F) = m(V(F))\) where V(F) is the set of vertices covered by F. One can easily check that \(\bar{m}\) is integer valued, non-decreasing and submodular. Thus, by Theorem 7, \(\bar {m}\) defines a matroid \(M_{\bar{m}}\). The following claim is straightforward.
Claim 2
The set {F⊆E:m(X)≥i F (X),∀X⊆V} is the set of independent sets of the matroid\(M_{\bar{m}}\).
3 Degree constrained sandwich problems
Before studying sandwich problems on orientations of given in-degrees, let us start as a warming up by considering sandwich problems for undirected and directed graphs of given degrees. These problems reduce to the undirected and directed f-factor problems. We mention that the directed case is much easier than the undirected case because the addition of an arc in a directed graph contributes only to the in-degree of the head and not of the tail, while the addition of an edge in an undirected graph contributes to the degree of both end-vertices. This section contains no new results, we added it for the sake of completeness.
3.1 Undirected graphs
Undirected Degree Constrained Sandwich ProblemInstance: Given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2 and a non-negative integer vector f on V. Question: Does there exist a sandwich graph G=(V,E) (E1⊆E⊆E2) such that d G (v)=f(v) for all v∈V?
Complexity: It is in P because the answer is Yes if and only if there exists an \((f(v)-d_{G_{1}}(v))\)-factor in the optional graph G0=(V,E0).
Characterization: The general f-factor theorem due to Tutte [25] can be applied to get a characterization.
Optimization: The minimum cost f-factor problem in undirected graphs can be solved in polynomial time, see Schrijver [20].
Simultaneous Undirected Degree Constrained Sandwich ProblemInstance: Given two edge-disjoint graphs G1=(V,E1) and G2=(V,E2) in G3=(V,E3) and two non-negative integer vectors f1 and f2 on V. Question: Do there exist simultaneously sandwich graphs \(\hat{G}_{1}=(V,\hat{E}_{1})\)\((E_{1}\subseteq\hat{E}_{1}\subseteq E_{3})\) and \(\hat{G}_{2}=(V,\hat{E}_{2})\)\((E_{2}\subseteq\hat{E}_{2}\subseteq E_{3})\) such that \(\hat{E}_{1}\cap\hat{E}_{2}=\emptyset\) and \(d_{\hat{G}_{1}}(v)=f_{1}(v)\) and \(d_{\hat{G}_{2}}(v)=f_{2}(v)\) for all v∈V?
Complexity: It is NP-complete because it contains as a special case whether there exist two edge-disjoint perfect matchings so 3-edge-colorability of 3-regular graphs. Indeed, let G=(V,E) be an arbitrary 3-regular graph. Let G1 and G2 be the edgeless graph on V, G3=G and f1(v)=f2(v)=1 for all v∈V. Then the sandwich graphs \(\hat{G}_{1}\) and \(\hat{G}_{2}\) exist if and only if \(\hat{E}_{1}\) and \(\hat{E}_{2}\) are edge-disjoint perfect matchings of G or equivalently, if there exists a 3-edge-coloring of G. Since the problem of 3-edge-colorability of 3-regular graphs is NP-complete [16], so is our problem.
3.2 Directed graphs
Directed Degree Constrained Sandwich ProblemInstance: Given directed graphs D1=(V,A1) and D2=(V,A2) with A1⊆A2 and a non-negative integer vector f on V. Question: Does there exist a sandwich graph D=(V,A) (A1⊆A⊆A2) such that \(d^{-}_{D}(v)=f(v)\) for all v∈V?
Complexity+Characterization: It is in P because the answer is Yes if and only if there exists a directed \((f(v)-d^{-}_{D_{1}}(v))\)-factor in the optional directed graph D0=(V,A0), hence we have the following.
Theorem 8
TheDirected Degree ConstrainedSandwich Problemhas aYesanswer if and only if\(d^{-}_{D_{2}}(v)\geq f(v)\geq d^{-}_{D_{1}}(v)\)for allv∈V.
Optimization: The feasible arc sets form the basis of a partition matroid, so the greedy algorithm provides a minimum cost solution.
Simultaneous Directed Degree ConstrainedSandwich Problem 1Instance: Given two arc-disjoint directed graphs D1=(V,A1) and D2=(V,A2) in D3=(V,A3) and two non-negative integer vectors f1 and f2 on V. Question: Do there exist simultaneously sandwich graphs \(\hat{D}_{1}=(V,\hat{A}_{1})\)\((A_{1}\subseteq\hat{A}_{1}\subseteq A_{3})\) and \(\hat{D}_{2}=(V,\hat{A}_{2})\)\((A_{2}\subseteq\hat{A}_{2}\subseteq A_{3})\) such that \(\hat{A}_{1}\cap\hat{A}_{2}=\emptyset\) and \(d^{-}_{\hat{D}_{1}}(v)=f_{1}(v)\) and \(d^{-}_{\hat{D}_{2}}(v)=f_{2}(v)\) for all v∈V?
Complexity: It is in P because the answer is Yes if and only if \(d^{-}_{D_{3}}(v)\geq f_{1}(v)+f_{2}(v)\), \(f_{1}(v)\geq d^{-}_{D_{1}}(v)\) and \(f_{2}(v)\geq d^{-}_{D_{2}}(v)\) for all v∈V.
Simultaneous Directed Degree ConstrainedSandwich Problem 2Instance: Given directed graphs D1=(V,A1) and D2=(V,A2) with A1⊆A2 and two non-negative integer vectors f and g on V. Question: Does there exist a sandwich graph D=(V,A) (A1⊆A⊆A2) such that \(d^{-}_{D}(v)=f(v)\) and \(d^{+}_{D}(v)=g(v)\) for all v∈V.
Complexity: The feasible arc sets for the in-degree constraint form the basis of a partition matroid and the feasible arc sets for the out-degree constraint form the basis of a partition matroid. The answer is Yes if and only if there exists a common basis in these two matroids. Thus it is in P by the matroid intersection algorithm of Edmonds [4].
4 Eulerian sandwich problems
In this section we consider first two problems that were already solved in [12]: Eulerian sandwich problems for undirected and directed graphs. We point out that the undirected case reduces to T-joins, while the directed case to circulations. We show that in both cases the simultaneous versions are NP-complete.
Then we propose to study the problem in mixed graphs. We show two cases that can be solved. The first case will be solved by the Discrete Separation Theorem 5 of Frank [9], while the second case reduces to the Directed Eulerian Sandwich Problem. The general case, however, remains open.
4.1 Undirected graphs
Undirected Eulerian Sandwich ProblemInstance: Given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2. Question: Does there exist a sandwich graph G=(V,E) (E1⊆E⊆E2) that is Eulerian?
Complexity: It is in P because the answer is Yes if and only if there exists a \(T_{G_{1}}\)-join in the optional graph G0.
Characterization: The answer is Yes if and only if each connected component of G0 contains an even number of vertices of \(T_{G_{1}}\).
Optimization: The minimum cost T-join problem can be solved in polynomial time [5].
Simultaneous Undirected Eulerian Sandwich ProblemInstance: Given two edge-disjoint graphs G1=(V,E1) and G2=(V,E2) in G3=(V,E3). Question: Do there exist simultaneously Eulerian sandwich graphs \(\hat{G}_{1}=(V,\hat{E}_{1})\)\((E_{1}\subseteq\hat{E}_{1}\subseteq E_{3})\) and \(\hat{G}_{2}=(V,\hat{E}_{2})\)\((E_{2}\subseteq\hat{E}_{2}\subseteq E_{3})\) such that \(\hat{E}_{1}\cap\hat{E}_{2}=\emptyset\)?
Complexity: It is NP-complete because it contains as a special case whether there exist two edge-disjoint perfect matchings so 3-colorability of 3-regular graphs. Indeed, let G=(V,E) be an arbitrary 3-regular graph. Let G3 be obtained from G by adding 2 edge-disjoint perfect matchings M1 and M2 to G, let G1=(V,M1) and G2=(V,M2). Then the Eulerian sandwich graphs \(\hat{G}_{1}\) and \(\hat{G}_{2}\) exist if and only if \(\hat{E}_{1}\setminus M_{1}\) and \(\hat{E}_{2}\setminus M_{2}\) are edge-disjoint perfect matchings of G or equivalently, if there exists a 3-edge-coloring of G. Since the problem of 3-edge-colorability of 3-regular graphs is NP-complete [16], so is our problem.
4.2 Directed graphs
Directed Eulerian Sandwich ProblemInstance: Given directed graphs D1=(V,A1) and D2=(V,A2) with A1⊆A2. Question: Does there exist a sandwich graph D=(V,A) (A1⊆A⊆A2) that is Eulerian?
Complexity: It is in P because it can be reformulated as a circulation problem: let f(e)=1,g(e)=1 if e∈A1 and f(e)=0,g(e)=1 if e∈A0. This way the arcs of A1 are forced and the arcs of A0 can be chosen if necessary.
Characterization: The answer is Yes if and only if \(d^{-}_{D_{1}}(X)\leq d^{+}_{D_{2}}(X)\) for all X⊆V by Theorem 1.
Optimization: The minimum cost circulation problem can be solved in polynomial time, see Tardos [23].
Simultaneous Directed Eulerian SandwichProblemInstance: Given two arc-disjoint directed graphs D1=(V,A1) and D2=(V,A2) in D3=(V,A3). Question: Do there exist simultaneously Eulerian sandwich graphs \(\hat{D}_{1}=(V,\hat{A}_{1})\)\((A_{1}\subseteq\hat{A}_{1}\subseteq A_{3})\) and \(\hat{D}_{2}=(V,\hat{A}_{2})\)\((A_{2}\subseteq\hat{A}_{2}\subseteq A_{3})\) such that \(\hat{A}_{1}\cap\hat{A}_{2}=\emptyset\)?
Complexity: It is NP-complete, it contains as a special case (D1=(V,t1s1), D2=(V,t2s2) and D3=D) the following directed 2-commodity integral flow problem that is NP-complete [6]: Given a directed graph D and two pairs of vertices, s1,t1 and s2,t2, decide whether there exist a path from s1 to t1 and a path from s2 to t2 that are arc-disjoint.
4.3 Mixed graphs
Mixed Eulerian Sandwich ProblemInstance: Given mixed graphs H1=(V,E1∪A1) and H2=(V,E2∪A2) with E1⊆E2,A1⊆A2. Question: Does there exist a sandwich mixed graph H=(V,E∪A) (E1⊆E⊆E2,A1⊆A⊆A2) that has an Eulerian orientation?
Complexity: We provide two special cases that can be treated, while the general problem remains open.
Special Case 1: E1=E2=E and \(d^{+}_{A_{2}}(X)-d^{-}_{A_{1}}(X)+\hat{d}_{E}(X)\) is even for all X⊆V.
Characterization+Complexity: We show that the problem is in P and we provide a characterization.
Theorem 9
TheMixed Eulerian Sandwich ProblemwithE1=E2=Eand\(d^{+}_{A_{2}}(X)-d^{-}_{A_{1}}(X)+\hat{d}_{E}(X)\)is even for allX⊆Vhas aYesanswer if and only if

In particular, this problem is in P.
Proof
By the result of Sect. 4.2, the answer is Yes if and only if there exists an orientation \(\vec{E}\) of E such that, ∀X⊆V, \(d^{-}_{A_{1}\cup\vec{E}}(X)\leq d^{+}_{A_{2}\cup\vec{E}}(X)\) or equivalently

Let m be the in-degree vector of \(\vec{E}\). Then \(d^{-}_{\vec{E}}(X)-d^{+}_{\vec{E}}(X)=\sum_{v\in X}(d^{-}_{\vec{E}}(v)-d^{+}_{\vec{E}}(v))=\sum_{v\in X}(2d^{-}_{\vec{E}}(v)-d_{E}(v))= 2m(X)-\hat{d}_{E}(X)\), and (12) becomes

Let \(b(X)=\frac{1}{2}(d^{+}_{A_{2}}(X)-d^{-}_{A_{1}}(X)+\hat{d}_{E}(X))\). Then b, being the sum of a modular function and a submodular function \((b(X)=\frac{1}{2}\sum_{v\in X}(d^{+}_{A_{1}}(v)-d^{-}_{A_{1}}(v)+d_{E}(v))+d^{+}_{A_{0}}(X))\), is a submodular function and, by the assumption, it is integer valued. By Theorem 3, an orientation \(\vec{E}\) satisfying (12) exists if and only if there exists a vector m such that i E (X)≤m(X)≤b(X), that is, by Claim 1 and Theorem 5, if and only if i E (X)≤b(X). This is equivalent to (11) and can be decided in polynomial time by Theorem 4, namely the submodular function b′(X)=b(X)−i E (X) must have minimum value 0. □
Special Case 2: E1=∅.
Characterization+Complexity: It is in P because it can be reformulated as the following problem: We create two copies of each edge in E2 and orient them in opposite directions. Denote this arc set by \(\overrightarrow{E^{2}_{2}}\). It is not difficult to see that the graph (V,E2∪A2) has a subgraph containing (V,A1) with an Eulerian orientation if and only if the graph \((V,\overrightarrow{E^{2}_{2}} \cup A_{2})\) has a directed Eulerian subgraph containing (V,A1). Indeed, in such a graph, if every edge of E2 is used at most once, we are done. If some edge of E2 is used twice, as two arcs in opposite directions, we can just remove these two arcs, the obtained graph remaining Eulerian and containing (V,A1). Now applying the result for Directed Eulerian Sandwich Problem we have
Theorem 10
TheMixed Eulerian Sandwich ProblemwithE1=∅ has aYesanswer if and only if

In particular, this problem is in P.
Proof
Let D1=(V,A1) and \(D_{2} = (V, A_{2} \cup\overrightarrow{E^{2}_{2}})\). By the arguments above, the Mixed Eulerian Sandwich Problem with E1=∅ has a solution if and only if there is an Eulerian sandwich graph for D1 and D2 or equivalently, \(d^{-}_{D_{1}}(X) \leq d^{+}_{D_{2}}(X)\) for all X⊆V. By \(d^{+}_{D_{2}}(X) = d^{+}_{A_{2}}(X)+ d_{E_{2}}(X)\), we have \(d^{-}_{A_{1}}(X) -d^{+}_{A_{2}}(X) \leq d_{E_{2}}(X)\) for all X⊆V. Note that \(d_{E_{2}}(X)+d^{+}_{A_{2}}(X)-d^{-}_{A_{1}}(X)\) is a submodular function, and hence by Theorem 4, (14) can be verified in polynomial time. □
5 m-orientation sandwich problems
In this section we consider the sandwich problem where the property Π is to have an orientation of given in-degrees.
5.1 m-Orientation
m-Orientation Sandwich ProblemInstance: Given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2 and a non-negative integer vector m on V. Question: Does there exist a sandwich graph G=(V,E) (E1⊆E⊆E2) that has an orientation \(\vec{G}\) whose in-degree vector is m that is \(d^{-}_{\vec{G}}(v)=m(v)\) for all v∈V?
Characterization: We prove the following theorem.
Theorem 11
The following assertions are equivalent.
-
(a)
Them-Orientation Sandwich Problemhas aYesanswer.
-
(b)
E1is independent in\(M_{\bar{m}}\)and\(M_{\bar{m}}\)has an independent set of sizem(V).
-
(c)
\(r_{\bar{m}}(E_{1}) = |E_{1}|\)and\(r_{\bar{m}}(E_{2})\geq m(V)\).
-
(d)
\(i_{E_{1}}(X) \leq m(X) \leq e_{E_{2}}(X)\)for allX⊆V.
Proof
(a) Implies (d). Let X⊆V. Since each edge of G1 in X contributes 1 to m(X), we have \(i_{E_{1}}(X) \leq m(X)\). On the other hand, the edges of G2 that have no end-vertex in X cannot contribute 1 to m(X), so we have \(m(X) \leq e_{E_{2}}(X)\).
(d) Implies (c). Let F be a subset of E1 and X=V(F). The condition \(i_{E_{1}}(X) \leq m(X)\) implies \(|F| \leq m(V(F)) = \bar{m}(F)\), that is, \(|E_{1}| \leq\bar{m}(F) + |E_{1}\setminus F|\). By Theorem 7, \(r_{\bar{m}}(E_{1}) \geq|E_{1}|\), or equivalently \(r_{\bar{m}}(E_{1}) = |E_{1}|\). Let now F be a subset of E2 and X=V∖V(F). The condition \(m(X) \leq e_{E_{2}}(X)\) implies that \(m(V) \leq m(V(F)) +e_{E_{2}}(V-V(F))\leq\bar{m}(F) + |E_{2}\setminus F|\). By Theorem 7, \(r_{\bar{m}}(E_{2}) \geq m(V)\).
(c) Implies (b). By definition.
(b) Implies (a). By (b), E1 is independent in \(M_{\bar{m}}\) and there exists an independent in \(M_{\bar{m}}\) of size m(V). Therefore, by (I3), there exists an independent set E of size m(V) that contains E1. By Theorem 3 and Claim 2, E is a solution of the m-orientation Sandwich Problem. □
We say that a subset F of E0 is feasible if (V,F∪E1) has an m-orientation. The next corollary of Theorem 11 characterizes the feasible sets.
Corollary 1
If them-Orientation Sandwich Problemhas aYesanswer, then a subsetFofE0is feasible if and only ifFis a base of the matroid\(M_{\bar{m}}/E_{1}\).
Complexity: The condition (d) of Theorem 11 can be verified in polynomial time by Theorem 4, so the m-Orientation Sandwich Problem is in P.
Optimization: The minimum cost version of the problem can be solved in polynomial time. First, we find an optimal feasible subset F by greedy algorithm. Then we can orient the edges of F∪E1 using a known algorithm. (See [10] for example.)
Corollary 1 and the matroid intersection algorithm of Edmonds [4] imply that the two following simultaneous versions of the m-orientation Sandwich Problem are also in P.
Simultaneousm-Orientation Sandwich Problem 1Instance: Given two edge-disjoint undirected subgraphs G1=(V,E1) and G2=(V,E2) of an undirected graph G3=(V,E3) and two non-negative integer vectors m1 and m2 on V. Question: Do there exist simultaneously edge-disjoint sandwich graphs \(\hat{G}_{1}=(V,\hat{E}_{1})\)\((E_{1}\subseteq\hat{E}_{1}\subseteq E_{3})\) and \(\hat{G}_{2}=(V,\hat{E}_{2})\)\((E_{2}\subseteq\hat{E}_{2}\subseteq E_{3})\) such that \(\hat{G}_{i}\) has an orientation whose in-degree vector is m i for i∈{1,2}?
Note that the two input matroids for the matroid intersection algorithm must be taken as \((M^{G_{1}}_{\bar{m}_{1}}/E_{1})\setminus E_{2}\) and the dual matroid of \((M^{G_{2}}_{\bar{m}_{2}}/E_{2})\setminus E_{1}\).
Simultaneousm-Orientation Sandwich Problem 2Instance: Given two undirected subgraphs G1=(V,E1) and G2=(V,E2) of an undirected graph G3=(V,E3) and two non-negative integer vectors m1 and m2 on V. Question: Does there exist an edge set F in E3∖(E1∪E2) such that the graph G i =(V,E i ∪F) admits an orientation whose in-degree vector is m i for i∈{1,2}?
5.2 Strongly connected m-orientation
Strongly Connectedm-Orientation Sandwich ProblemInstance: Given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2 and a non-negative integer vector m on V. Question: Does there exist a sandwich graph G=(V,E) (E1⊆E⊆E2) that has a strongly connected orientation \(\vec{G}\) whose in-degree function is m?
Complexity: It is NP-complete because the special case E1=∅,m(v)=1∀v∈V is equivalent to decide if G2 has a Hamiltonian cycle.
5.3 (m1,m2)-orientation
(m1,m2)-Orientation Sandwich ProblemInstance: Given undirected graphs G1=(V,E1) and G2=(V,E2) with E1⊆E2 and non-negative integer vectors m1 and m2 on V. Question: Does there exist a sandwich graph G=(V,E) (E1⊆E⊆E2) that has an orientation \(\vec{G}\) whose in-degree vector is m1 and whose out-degree vector is m2?
Complexity: The problem is NP-complete since it contains as a special case (E1=∅) the NP-complete problem of [19].
5.4 Mixed m-orientation
Mixedm-Orientation Sandwich ProblemInstance: Given mixed graphs G1=(V,E1∪A1) and G2=(V,E2∪A2) with E1⊆E2, A1⊆A2 and an non-negative integer vector m on V. Question: Does there exist a sandwich mixed graph G=(V,E∪A) with E1⊆E⊆E2 and A1⊆A⊆A2 that has an orientation \(\overrightarrow {G}=(V,\overrightarrow{E} \cup A)\) whose in-degree vector is m?
Characterization: Suppose that E1⊆E⊆E2 has been chosen and oriented, then the problem is reduced to the Directed Degree Constrained Sandwich Problem with \(m_{1}(v)=m(v) - d^{-}_{\overrightarrow{E}}(v)\) which, by Theorem 8, has a solution if and only if \(d^{-}_{A_{2}}(v) \geq m(v) -d^{-}_{\overrightarrow{E}}(v) \geq d^{-}_{A_{1}}(v)\) for all v∈V. Hence the Mixedm-orientation Sandwich Problem has a solution if and only if there exists E1⊆E⊆E2 which admits an orientation \(\overrightarrow{E}\) with \(m(v)-d^{-}_{A_{1}}(v) \geq d^{-}_{\overrightarrow{E}}(v) \geq m(v)-d^{-}_{A_{2}}(v)\) for all v∈V. Let m2:V→ℤ satisfy \(m(v)-d^{-}_{A_{2}}(v)\leq m_{2}(v)\leq m(v)-d^{-}_{A_{1}}(v)\). By Theorem 11, there exists E1⊆E⊆E2 which admits an orientation \(\overrightarrow {E}\) with \(d^{-}_{\overrightarrow{E}}(v) = m_{2}(v)\) if and only if \(i_{E_{1}}(X) \leq m_{2}(X) \leq e_{E_{2}}(X)\) for all X⊆V. Therefore we have
Claim 3
TheMixedm-orientation Sandwich Problemhas aYesanswer if and only if there exists an integer-valued functionm2:V→ℤ such that, ∀v∈Vand ∀X⊆V,

Claim 4
The pair\((i_{E_{1}}, e_{E_{2}})\)is a strong pair.
Proof
Let X,Y,Z be three pairwise disjoint subset of V. We show that \(e_{E_{2}}(X\cup Z)-i_{E_{1}}(Y\cup Z) \geq e_{E_{2}}(X) - i_{E_{1}}(Y)\). In fact, we have \(i_{E_{1}}(Y\cup Z) - i_{E_{1}}(Y) = i_{E_{1}}(Z) +d_{E_{1}}(Y,Z) \leq i_{E_{2}}(Z) + d_{E_{2}}(Y,Z)\), and \(e_{E_{2}}(X\cup Z) -e_{E_{2}}(X) = i_{E_{2}}(Z) + d_{E_{2}}(Z) - d_{E_{2}}(X,Z)\). As X,Y,Z are pairwise disjoint, \(d_{E_{2}}(Y,Z) + d_{E_{2}}(X,Z) \leq d_{E_{2}}(Z)\). The claim follows by Claim 1. □
By Claim 3, 4 and Theorem 6 applied for \(\alpha(v)= m(v)-d^{-}_{A_{2}}(v), \beta (v)=m(v)-d^{-}_{A_{1}}(v), p=i_{E_{1}}, b=e_{E_{2}}\), we have
Theorem 12
TheMixedm-orientation Sandwich Problemhas aYesanswer if and only if

for every subsetXofV.
Note that Theorem 12 implies Theorems 8 and 11.
Complexity: The condition (15) can be verified in polynomial time by Theorem 4. If it is satisfied, then a vector m2 satisfying the conditions in Claim 3 can be found using a greedy algorithm for g-polymatroids. Then we find and orient an edge set E (E1⊆E⊆E2) with in-degree m2 (m-orientation Sandwich Problem). Last, we choose an arc set A (A1⊆A⊆A2) such that \(d^{-}_{A}(v)=m_{1}(v)=m(v)-m_{2}(v)\), for all v∈V (Directed Degree Constrained Sandwich Problem).
6 Contracting sandwich problems
In this section, we propose to consider a new type of sandwich problem. Instead of deleting edges from the optional graph, we are interested in contracting edges. We solve the problem for the property Π being a bipartite graph.
Contracting Sandwich ProblemInstance: Given an undirected graph G=(V,E) and E0⊆E. Question: Does there exist F⊆E0 such that contracting F results in a bipartite graph?
Complexity: Since a graph is bipartite if and only if all its cycles have an even length, the problem is equivalent to finding F⊆E0 such that, for all cycles C, |C∩F|≡|C| mod 2.
Fix a spanning forest T of G. For e∈E∖T, denote C(T,e) the unique cycle contained in T∪e. By [18, Theorem 9.1.2], if C is a cycle of G then C=Δe∈CC(T,e), where Δ denotes the symmetric difference of sets. Therefore, |C∩F|≡∑e∈C|C(T,e)∩F| mod 2. Let \(\mathcal{C}_{T}\) denote the collection of cycles C(T,e) of G. The problem is reduced to finding F⊆E0 such that, for all \(C\in\mathcal{C}_{T}\), |C∩F|≡|C| mod 2, or equivalently, finding an F′(=E∖F)⊇E1=E∖E0 such that |F′∩C|≡0 mod 2, for all \(C\in\mathcal{C}_{T}\).
Consider now the matrix M defined as the following. The rows of M correspond to \(C \in\mathcal{C}_{T}\) and the columns correspond to the edges of G; the entry M Ce is 1 if e∈C and is 0 otherwise. For X⊆E, let χ X denote the characteristic vector of X. For a vector x∈{0,1}E, let x|X denote the projection of x on X. Let 1 be the all-one vector in {0,1}E. A subset F′⊆E satisfies |F′∩C|≡0 mod 2, for all \(C\in\mathcal{C}_{T}\), if and only if χF′∈KerM in \(\mathbb{F}_{2}\). Such an F′ is the solution of the Contracting Sandwich Problem if and only if \(\chi_{F'|E_{1}} = \mathbf {1}_{|E_{1}}\).
Let B be a basis of the kernel of M in \(\mathbb{F}_{2}\). (This can be computed in polynomial time using the Gauss elimination.) Consider the projections B′ of B on E1. Then the Contracting Sandwich Problem has a solution if and only if \(\mathbf{1}_{|E_{1}}\) is in the subspace of \(\{0,1\}^{E_{1}}\) spanned by B′, that is, \(\mathrm{rank} B'= \mathrm{rank} B'\cup\mathbf{1}_{|E_{1}}\). This can be decided in polynomial time using the Gauss elimination. We conclude that the Contracting Sandwich Problem is in P.
We finish with a related problem. For a fixed integer k, solving the Contracting Sandwich Problem when E0=E with extra requirement |F|≤k is known to be tractable in polynomial time [14]. However, the authors mention that finding a solution of minimum cardinality is NP-complete.
References
Dantas S, Klein S, Mello CP, Morgana A (2009) The graph sandwich problem for P4-sparse graphs. Discrete Math 309:3664–3673
Dantas S, Figueiredo CMH, Golumbic MC, Klein S, Maffray F (2011) The chain graph sandwich problem. Ann Oper Res 188:133–139
Dourado M, Petito P, Teixeira RB, Figueiredo CMH (2008) Helly property, clique graphs, complementary graph classes, and sandwich problems. J Braz Comput Soc 14:45–52
Edmonds J (1977) Matroid intersection. Discrete Optim 4:39–49 (Proc Adv Res Inst Discrete Optimization and Systems Appl, Banff, Alta)
Edmonds J, EL Johnson (1973) Matching, Euler tours and the Chinese postman. Math Program 5:88–124
Even S, Itai A, Shamir A (1976) On the complexity of timetable and multicommodity flow problems. SIAM J Comput 5:691–703
Figueiredo CMH, Faria L, Klein S, Sritharan R (2007) On the complexity of the sandwich problems for strongly chordal graphs and chordal bipartite graphs. Theor Comput Sci 38:57–67
Ford LR, Fulkerson DR (1962) Flows in Networks. Princeton University Press, Princeton
Frank A (1982) An algorithm for submodular functions on graphs. Ann Discrete Math 16:97–120
Frank A, Gyárfás A (1976) How to orient the edges of a graph. Colloq Math Soc János Bolyai 18:353–364
Frank A, Tardos E (1988) Generalized polymatroids and submodular flows. Submodular optimization. Math Program 42(3):489–563
Golumbic MC, Kaplan H, Shamir R (1995) Graph sandwich problems. J Algorithms 19(3):449–473
Hakimi SL (1965) On the degrees of the vertices of a directed graph. J Franklin Inst 279(4):290–308
Heggernes P, van’t Hof P, Lokshtanov D, Paul C (2011) Obtaining a bipartite graph by contracting few edges. In: Proceedings of IARCS annual conference on foundations of software technology and theoretical computer science, pp 217–228
Hoffman AJ (1960) Some recent applications of the theory of linear inequalities to extremal combinatorial analysis. Proc Symp Appl Math 10:113–127
Holyer I (1981) The NP-completeness of edge-coloring. SIAM J Comput 10(4):718–720
Iwata S, Fleischer L, Fujishige S (2001) A combinatorial strongly polynomial algorithm for minimizing submodular functions. J ACM 48(4):761–777
Oxley JG (1992) Matroid theory. Oxford University Press, New York
Pálvölgyi D (2009) Deciding soccer scores and partial orientations of graphs. Acta Univ Sapientiae, Math 1(1):35–42
Schrijver A (2003) Combinatorial optimization: polyhedra and efficiency. Algorithms and combinatorics, vol 24. Springer, Berlin
Schrijver A (2000) A combinatorial algorithm minimizing submodular functions in strongly polynomial time. J Comb Theory, Ser B 80(2):346–355
Sritharan R (2008) Chordal bipartite completion of colored graphs. Discrete Math 308:2581–2588
Tardos E (1985) A strongly polynomial minimum cost circulation algorithm. Combinatorica 5(3):247–255
Teixeira RB, Dantas S, Figueiredo CMH (2010) The polynomial dichotomy for three nonempty part sandwich problems. Discrete Appl Math 158:1286–1304
Tutte WT (1952) The factors of graphs. Can J Math 4:314–328
Acknowledgements
This research was partially supported by CNPq, CAPES (Brazil)/COFECUB (France), FAPERJ.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Durand de Gevigney, O., Klein, S., Nguyen, VH. et al. Sandwich problems on orientations. J Braz Comput Soc 18, 85–93 (2012). https://doi.org/10.1007/s13173-012-0065-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13173-012-0065-7
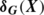 . The degree
. The degree (or d
E
(X)) of X is the cardinality of the cut induced by X, that is, d
G
(X)=|δ
G
(X)|. The number of edges between X
(or d
E
(X)) of X is the cardinality of the cut induced by X, that is, d
G
(X)=|δ
G
(X)|. The number of edges between X . The number of edges of G having both (resp. at least one) end-vertices in X is denoted by
. The number of edges of G having both (resp. at least one) end-vertices in X is denoted by  or i
E
(X) or simply i(X) (resp.
or i
E
(X) or simply i(X) (resp.  ). It is well-known that (
). It is well-known that (
 (resp.
(resp. 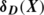 ). The in-degree
). The in-degree (resp. out-degree
(resp. out-degree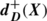 ) of X is the number of arcs of D entering (resp. leaving) X, that is
) of X is the number of arcs of D entering (resp. leaving) X, that is  . The following equality will be used frequently without reference:
. The following equality will be used frequently without reference: