- Original Paper
- Open access
- Published:
b-Coloring graphs with large girth
Journal of the Brazilian Computer Society volume 18, pages 375–378 (2012)
Abstract
A b-coloring of a graph is a coloring of its vertices such that every color class contains a vertex that has a neighbor in all other classes. The b-chromatic number of a graph is the largest integer k such that the graph has a b-coloring with k colors. We show how to compute in polynomial time the b-chromatic number of a graph of girth at least 9. This improves the seminal result of Irving and Manlove on trees.
1 Introduction
Let G be a simple graph. A proper coloring of G is an assignment of colors to the vertices of G such that no two adjacent vertices have the same color. The chromatic number of G is the minimum integer χ(G) such that G has a proper coloring with χ(G) colors. Suppose that we have a proper coloring of G and there exists a color h such that every vertex x with color h is not adjacent to at least one other color (which may depend on x); then we can change the color of these vertices and thus obtain a proper coloring with fewer colors. This heuristic can be applied iteratively, but we cannot expect to reach the chromatic number of G, since the coloring problem is  -hard. On the basis of this idea, Irving and Manlove introduced the notion of b-coloring in [15]. Intuitively, a b-coloring is a proper coloring that cannot be improved by the above heuristic, and the b-chromatic number measures the worst possible such coloring. More formally, consider any vertex coloring of G. A vertex u is said to be a b-vertex (for this coloring) if u has a neighbor colored with each color different from its own color. A b-coloring of G is a proper coloring of G such that each color class contains a b-vertex. A basis of a b-coloring is a set of b-vertices, one for each color class. The b-chromatic number of G is the largest integer k such that G has a b-coloring with k colors. We denote it by χ
b
(G).
-hard. On the basis of this idea, Irving and Manlove introduced the notion of b-coloring in [15]. Intuitively, a b-coloring is a proper coloring that cannot be improved by the above heuristic, and the b-chromatic number measures the worst possible such coloring. More formally, consider any vertex coloring of G. A vertex u is said to be a b-vertex (for this coloring) if u has a neighbor colored with each color different from its own color. A b-coloring of G is a proper coloring of G such that each color class contains a b-vertex. A basis of a b-coloring is a set of b-vertices, one for each color class. The b-chromatic number of G is the largest integer k such that G has a b-coloring with k colors. We denote it by χ
b
(G).
Naturally, a proper coloring of G with χ(G) colors is a b-coloring of G, since it cannot be improved. Hence, χ(G)≤χ b (G). For an upper bound, observe that if G has a b-coloring with k colors, then G has at least k vertices with degree at least k−1 (a basis of the b-coloring). Thus, if m(G) is the largest integer such that G has at least m(G) vertices with degree at least m(G)−1, we know that G cannot have a b-coloring with more than m(G) colors, i.e.,

This upper bound was introduced by Irving and Manlove in [15]. They showed that the difference between χ b (G) and m(G) can be arbitrarily large for general graphs. They proved that χ b (G) is equal to m(G) or m(G)−1 when G is a tree, and provided a polynomial time algorithm that computes χ b (G) for every tree. In addition, the problem was proved to be NP-hard in general graphs [15], and remains so even when restricted to bipartite graphs [22]. These concepts have received much attention recently; for example, see [1–27].
Many of these works investigate the b-chromatic number of graphs under assumptions that involve the existence of large cycles. For example, Irving and Manlove’s algorithm for trees can actually work on graphs with girth at least 11, as noticed by A. Silva in [26]. Also, there are a number of results about d-regular graphs with girth at least 5 [3, 6, 18, 22, 23]. In this paper we improve Irving and Manlove’s result for graphs with large girth; more specifically, we prove the following.
Theorem 1
If G is a graph with girth at least 9, then χ b (G)≥m(G)−1.
Here is an outline of the proof of Theorem 1. A special set of vertices, called a good set of vertices, is defined and graphs are distinguished between having a good set and not having a good set. Next, we state some results by Irving and Manlove [15] and by Silva [26] that say that a graph G with girth(G)≥8 that does not have a good set cannot be b-colored with m(G) colors and has a b-coloring with m(G)−1 colors (hence, χ b (G)=m(G)−1); also, Silva proved that if G with girth at least 8 has a good set, then one can be found in polynomial time. Finally, and this is the original part of the paper, it is shown that if G with girth at least 9 has a good set, then χ b (G)=m(G). The proof of Theorem 1 yields a polynomial time algorithm that finds an optimal b-coloring of graphs with girth at least 9.
2 Definitions and partial results
In this section, we present some necessary definitions and the results by Irving and Manlove [15] and A. Silva [26] that complement our proof. The graph terminology used in this paper follows [4].
Let G be a simple graph. We denote by V(G) and E(G) the sets of vertices and edges of G, respectively. If X⊆V(G), then NX(u) represents the set N(u)∩X. The girth ofG is the size of a shortest induced cycle of G.
Recall that m(G) is the largest integer k such that G has at least k vertices with degree at least k−1. We say that a vertex u∈V(G) is dense if d(u)≥m(G)−1; and we denote the set of dense vertices of G by M(G).
Let W be a subset of M(G), and let u be any vertex in V(G)∖W. If u is such that every vertex v∈W is either adjacent to u or has a common neighbor w∈W with u such that d(w)=m(G)−1, then it is said that Wencircles vertexu (or that u is encircled by W). A subset W of M(G) of size m(G) is a good set if (our definition is slightly different from the one given by Irving and Manlove):
-
(a)
W does not encircle any vertex, and
-
(b)
Every vertex x∈V(G)∖W with d(x)≥m(G) is adjacent to a vertex w∈W.
Theorem 2
[15]
LetGbe any graph andWbe a subset ofM(G) withm(G) vertices. IfWencircles some vertexv∈V(G)∖W, thenWis not a basis of a b-coloring withm(G) colors.
Theorem 3
[26]
IfGis a graph with girth at least 8, thenGdoes not have a good set if and only if |M(G)|=m(G) andM(G) encircles a vertex inV(G)∖M(G). Moreover, a good set ofG (if any exists) can be found in polynomial time.
A part of the proof of Theorem 1 consists of the following theorem:
Theorem 4
[26]
LetGbe a graph with girth at least 8. IfGhas no good set, thenχ b (G)=m(G)−1.
Now, all we need to prove is that if G does have a good set, then G can be b-colored with m(G) colors, which is done in the next section.
3 Coloring graphs with a good set
In this section we prove the second part of the main theorem, namely:
Theorem 5
LetGbe a graph with girth at least 9. IfGhas a good set, thenχ b (G)=m(G).
Let W={v1,…,vm(G)} be a good set of G. Our aim is to construct a b-coloring of G with m(G) colors such that, for each i∈{1,…,m(G)}, vertex v i is a b-vertex of color i. We start by assigning color i to v i , for each i∈{1,…,m(G)}. Next, we extend this partial coloring to the rest of the graph in several steps. Before explaining each step, we need to introduce some other terminology and notation.
A link is any path of length two or three whose extremities are in W and whose internal vertices are not in W. Any interior vertex of a link is called a link vertex. Let L be the set of all link vertices.
We first color G[W∪L] in a way not to repeat too many colors in N(w), for all w∈W, and at the end we extend the obtained partial coloring to a b-coloring of G with m(G) colors. Let G′=G[W∪L], L1 be the set of vertices of L that have at least one neighbor in L and L2 be the set of vertices in L that have at least two neighbors in W. The steps below are followed in order in such a way that we only move on to the next step when all the possible vertices are iterated.
-
1.
For each x∈L1, let x′∈NL(x). Since x′∈L, there must exist v i ∈NW(x′); color x with i;
-
2.
For each v i ∈W, let
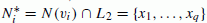 . Also, let
. Also, let 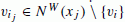 . If q>1, then use colors i1,…,i
q
to color the uncolored vertices in
. If q>1, then use colors i1,…,i
q
to color the uncolored vertices in  in a way that x
j
is not colored with i
j
(it suffices to make a derangement of those colors on the vertices);
in a way that x
j
is not colored with i
j
(it suffices to make a derangement of those colors on the vertices); -
3.
Let x∈L2 still uncolored be such that there exists v i ∈NW(x) that has some neighbor y∈L1. Let c be the color of y; color x with c and recolor y with j, for any v j ∈NW(x)∖{v i };
-
4.
Finally, if x∈L2 is still uncolored, we know that NL(v i )={x}, for all v i ∈NW(x). Since NL(x)=∅, we can color x with i, for any v i that is not adjacent to x and has no common neighbor with x in W of degree m(G)−1, which exists as x is not encircled by W.
Suppose that the algorithm above produces a partial coloring that colors every vertex in L in such a way that, at the end, each v i ∈W has at least as many uncolored neighbors as missing colors in its neighborhood. Since L is colored, we know that the uncolored neighbors of W form a stable set. Thus, we can independently color N(v i ) in such a way that v i sees every other color, for all v i ∈W. By the definition of a good set, we know that if d(v)≥m(G), then v is already colored; hence, the partial coloring can be greedily transformed into a b-coloring with m(G) colors. Now, to prove that the algorithm works, we show that after these steps the obtained partial coloring ψ satisfies:
P1 ψ is proper; and
P2 the number of uncolored neighbors of v i is at least the number of missing colors in N(v i ), for each v i ∈W.
Proof of Theorem 5
First, we make some observations concerning the coloring procedure. Note that L1∩L2 is not necessarily empty, but all vertices in this subset are colored in Step 1. However, a vertex x∈L1∩L2 may play a role in Step 2 in the following way: if x∈N(v
i
) and there exists  , then x′ may be colored with color j for some v
j
∈NW(x)∖{v
i
}, while the color of x remains unchanged. Also, note that, in Step 3, since
, then x′ may be colored with color j for some v
j
∈NW(x)∖{v
i
}, while the color of x remains unchanged. Also, note that, in Step 3, since  , we have y∈L1∖L2. Hence, NW(y)={v
i
} and, consequently, the color of y cannot be changed again. Thus (*) the color of y is changed at most once, for every y∈L1. Finally, if x receives color i in Step 1, 2 or 3, then one of the following holds (fact (iii) holds because of (*)):
, we have y∈L1∖L2. Hence, NW(y)={v
i
} and, consequently, the color of y cannot be changed again. Thus (*) the color of y is changed at most once, for every y∈L1. Finally, if x receives color i in Step 1, 2 or 3, then one of the following holds (fact (iii) holds because of (*)):
-
(i)
x receives color i in Step 1 and there exists a path 〈x,x′,v i 〉, for some x′∈L1; or
-
(ii)
x receives color i in Step 2 and there exists a path 〈x,v j ,x′,v i 〉, for some v j ∈W and x′∈L2; or
-
(iii)
x receives color i in Step 3 and there exists a path 〈x,v j ,y,y′,v i 〉, for some v j ∈W, y∈L1∖L2 and y′∈L1; or
-
(iv)
x is recolored with color i in Step 3 and there exists a path 〈x,v j ,x′,v i 〉, for some v j ∈W and x′∈L2∖L1.
We first prove that P1 holds after Step 3. Suppose that there exists an edge wz such that ψ(w)=ψ(z)=i. Since G has no cycle of length at most 7, the paths defined in (i)–(iv) are shortest paths. Therefore, vertex v i has no neighbor colored i and hence, w,z∈L. Also, as wz∈E(G), we have w,z∈L1 and they are colored in Step 1 and maybe recolored in Step 3. By (i) and (iv), there exist a w,v i -path P w and a z,v i -path P z , both of length at most 3. Note that either P w +P z +wz contains a cycle of length at most 7 or one of these paths consists of the edge wz followed by the other path. Because G has girth at least 9, the latter case occurs. We get as contradiction as this implies that at least one path is defined by (i) and, thus, vertex v i has a neighbor colored i.
Now, we prove that P2 also holds after Step 3. We actually prove that, after Step 3, no color is repeated in N(v i ), for each v i ∈W. Suppose there exist a vertex v j ∈W and w,z∈N(v j ) such that ψ(w)=ψ(z)=i. First, consider the case v i ∈{w,z}. Since the paths defined by (i)–(iv) are shortest paths, we see that (i) occurs for the vertex in {w,z}∖{v i }. We get a contradiction as this implies G has a cycle of length 4. Therefore we may assume v i ∉{w,z}.
Now, by (i)–(iv), there exist a w,v
i
-path P
w
and a z,v
i
-path P
z
. Let ℓ
w
and ℓ
z
be the length of P
w
and P
z
, respectively. Clearly ℓ
w
,ℓ
z
≤4. Note that either P
w
+P
z
+〈w,v
j
,z〉 contains a cycle of length at most ℓ
w
+ℓ
z
+2 or either P
w
or P
z
consists of the path 〈w,v
j
,z〉 followed by the other path. Since both w and z are at distance at least 2 from v
i
and ℓ
w
,ℓ
z
≤4, the latter can only occur if one of the paths is defined by (i), say P
w
, and the other is defined by (iii), say P
z
. We get a contradiction as P
z
=〈z,v
j
,w,y,v
i
〉 implies w is recolored in Step 3 and therefore, P
w
must be defined by (iv). Now, suppose that the former occurs, i.e., P
w
+P
z
+〈w,v
j
,z〉 contains a cycle of length at most ℓ
w
+ℓ
z
+2. Because G has girth at least 9, we have ℓ
w
+ℓ
z
≥7. This implies that at least one of P
w
and P
z
, say P
z
, is defined by (iii), and the other is not defined by (i). Therefore z is colored in Step 3 and  . Furthermore, w∈L1∖L2 and NW(w)={v
j
}. Therefore, since (i) does not occur for w, we find that P
w
must be defined by (iv). Thus the only choice for P
w
is 〈w,v
j
,z,v
i
〉, a contradiction as P1 holds.
. Furthermore, w∈L1∖L2 and NW(w)={v
j
}. Therefore, since (i) does not occur for w, we find that P
w
must be defined by (iv). Thus the only choice for P
w
is 〈w,v
j
,z,v
i
〉, a contradiction as P1 holds.
Finally, consider x to be colored during Step 4 with color i. By the choice of i we know that v i ∉N(x). Thus, since NL(x)=∅, Property P1 holds. Now, suppose that some v j ∈N(x) is such that color i already appears in N(v j ). Since NL(v j )={x} we must have v i ∈N(v j ) and, by the choice of i, d(v j )>m(G)−1. Property P2 thus follows as i is the only repeated color in the neighborhood of v j . □
4 Conclusion
We showed that if G is a graph with girth at least 9, then χ b (G)≥m(G)−1, improving the result by Irving and Manlove [15]. We also give an algorithm that finds the b-chromatic number of G in polynomial time.
In [25], Maffray and Silva conjecture that any graph G with no K2,3 as subgraph has b-chromatic number at least m(G)−1. Observe that these graphs contain all graphs with girth at least 9; thus, we have given a partial answer to their conjecture. Actually, if their conjecture holds, then χ b ≥m(G)−1 holds for every G with girth at least 5. However, a different approach is needed as our proof strongly relies on the fact that girth(G)≥9. Moreover, Theorem 5 does not hold for an infinite family of cacti with girth 5, as can be seen in [7]. This means that the situation where G has no good set is not the only situation where a graph G with girth at least 5 cannot be b-colored with m(G) colors.
References
Balakrishnan R, Francis Raj S (2009) Bounds for the b-chromatic number of vertex-deleted subgraphs and the extremal graphs (extended abstract). Electron Notes Discrete Math 34:353–358
Barth D, Cohen J, Faik T (2007) On the b-continuity property of graphs. Discrete Appl Math 155:1761–1768
Blidia M, Maffray F, Zemir Z (2009) On b-colorings in regular graphs. Discrete Appl Math 157(8):1787–1793
Bondy A, Murty USR (2008) Graph theory. Springer, Berlin
Bonomo F, Duran G, Maffray F, Marenco J, Valencia-Pabon M (2009) On the b-coloring of cographs and P4-sparse graphs. Graphs Comb 25(2):153–167
Cabello S, Jakovac M (2011) On the b-chromatic number of regular graphs. Discrete Appl Math 159(3):1303–1310
Campos V, Linhares Sales C, Maffray F, Silva A (2009) b-chromatic number of cacti. Electron Notes Discrete Math 35:281–286
Chaouche F, Berrachedi A (2007) Some bounds for the b-chromatic number of a generalized Hamming graphs. Far East J Appl Math 26:375–391
Corteel S, Valencia-Pabon M, Vera J-C (2005) On approximating the b-chromatic number. Discrete Appl Math 146:106–110
Effantin B (2005) The b-chromatic number of power graphs of complete caterpillars. J Discrete Math Sci Cryptogr 8:483–502
Effantin B, Kheddouci H (2003) The b-chromatic number of some power graphs. Discrete Math Theor Comput Sci 6:45–54
Effantin B, Kheddouci H (2005) Exact values for the b-chromatic number of a power complete k-ary tree. J Discrete Math Sci Cryptogr 8:117–129
Hajiabolhassan H (2010) On the b-chromatic number of Kneser graphs. Discrete Appl Math 158:232–234
Hoang CT, Kouider M (2005) On the b-dominating coloring of graphs. Discrete Appl Math 152:176–186
Irving RW, Manlove DF (1999) The b-chromatic number of a graph. Discrete Appl Math 91:127–141
Javadi R, Omoomi B (2009) On b-coloring of the Kneser graphs. Discrete Math 309:4399–4408
Jakovac M, Klavzar S (2010) The b-chromatic number of cubic graphs. Graphs Comb 26:107–118
Kouider M (2004) b-chromatic number of a graph, subgraphs and degrees. Technical report 1392, Université Paris Sud
Kouider M, Maheo M (2002) Some bounds for the b-chromatic number of a graph. Discrete Math 256:267–277
Kouider M, Maheo M (2007) The b-chromatic number of the Cartesian product of two graphs. Studia Sci Math Hung 44:49–55
Kouider M, Zaker M (2006) Bounds for the b-chromatic number of some families of graphs. Discrete Math 306:617–623. Acho q a nica mudana q tu ainda n
Kratochvíl J, Tuza Zs, Voigt M (2002) On the b-chromatic number of graphs. Lect Notes Comput Sci 2573:310–320
Kouider M, Sahili AE (2006) About b-colouring of regular graphs. Technical report 1432, Université Paris Sud
Shaebani S On the b-chromatic number of regular graphs without 4-cycles. arXiv:1103.1521v1
Maffray F, Silva A (2012, to appear) b-colouring outerplanar graphs with large girth. Discrete Math
Silva A (2010) The b-chromatic number of some tree-like graphs. PhD thesis, Université de Grenoble
Velasquez CIB, Bonomo F, Koch I (2011) On the b-coloring of P4-tidy graphs. Discrete Appl Math 159:60–68
Acknowledgements
This work has been partially supported by Funcap (Fundação Cearense de Apoio ao Desenvolvimento Científico e Tecnológico) and CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Campos, V., de Farias, V.A.E. & Silva, A. b-Coloring graphs with large girth. J Braz Comput Soc 18, 375–378 (2012). https://doi.org/10.1007/s13173-012-0063-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13173-012-0063-9
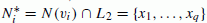 . Also, let
. Also, let 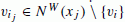 . If q>1, then use colors i1,…,i
q
to color the uncolored vertices in
. If q>1, then use colors i1,…,i
q
to color the uncolored vertices in  in a way that x
j
is not colored with i
j
(it suffices to make a derangement of those colors on the vertices);
in a way that x
j
is not colored with i
j
(it suffices to make a derangement of those colors on the vertices);